Class-9 Trigonometry Worksheet 3

1. From the below given figure, find the value of:


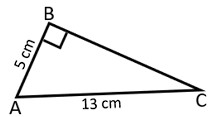
a) Sin A                        b) Cot A
c) Cos C                      d) Sin²A + Cos²A

2. If 3 Tan A = 4, then find the value of:


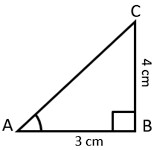
a) Cos A                     b) Cosec A
c) Sec A − Tan A        d) Sec²A − ¹⁄_Cot²A

3. From the below given figure, if Sin α = ¹²⁄₁₃ and Cos β = ³⁄₅ then find the length of AD.

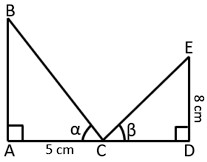
4. If Sin θ = ¹²⁄₁₃ and θ is less than 90^o, find the value of Cot θ + Tan θ.

5. If Tan θ = ⁵⁄₁₂, find the value of Cos θ + Cosec θ.

6. If 5 Sin θ = 4, find the value of ^(1+Cosθ)⁄_(1−Cosθ).

7. If 5 Tan θ = 12, find the value of ^{(5Sinθ−3Cosθ)}⁄_{(5Sinθ+2Cosθ)}.

8. If 5 Tan θ = 4, find the value of ^{(5Sinθ−3Cosθ)}⁄_{(5Sinθ+2Cosθ)}.

9. If 13 Cos A = 12 and angle A is acute, find the value of ^{(5SinA−2CosA)}⁄_{Tan A}.

10. If 5 Cos θ − 12 Sin θ = 0, then find the value of ^{(Sin θ + Cos θ)}⁄_{(2 Cos θ − Sin θ)}.

11. In a right-angled triangle ABC, ∠A = 90^o. If AB = 7 cm and BC − AC = 1 cm, then find:

a) Cosec C                    b) Cot B

12. In a right-angled triangle ABC, ∠B = 90^o. If AB = 40 cm and AC + BC = 50 cm, then find:

a) Cos A                     b) Tan C

13. If 4 Sin θ = 3 Cos θ, then find:

a) Cot² θ − Cosec² θ
b) 4 Cos² θ − 3 Sin² θ + 2

14. Find the value of:

a) Sin² 60^o + Cos² 30^o
b) Sin 30^o Cos 60^o
c) Cosec² 60^o − Tan² 30^o
d) Sin² 60^o + Cosec² 30^o + Tan² 45^o

15. Find the value of:

a) Sin 60^o Cos 30^o + Sin 30^o Cos 60^o
b) Cos 30^o Cos 60^o − Sin 30^o Sin 60^o
c) Cosec² 45^o − Cot² 45^o
d) 3 Cosec² 60^o − 2 Cot² 30^o + Sec² 45^o

16. If θ = 15^o then find the value of ^{(Cos 3θ − 2 Cos 4θ)}⁄_{(Sin 3θ + 2 Sin 4θ)}.

17. If p = 30^o, then find the value of 4 Cos³ p − 3 Cos p.

18. If q = 30^o, then find the value of 4 Cos q × Cos (60^o − q) × Cos (60^o + q).

19. Find the value of A:

a) Sin 3A = ^√3⁄₂                b) 2 Sin 3A = 2
c) Tan 3A = 1                    d) Not defined

20. Find the value of q:

a) 2 Sin 3q − 1 = 0
b) Sin (q + 10^o) = ¹⁄₂
c) 2 Sec (3q − 15^o) = 4
d) Sin² q + Sin² 30^o = 1

If you want to download the above worksheet, please click below link.

Trigonometry Worksheet-3Download the pdf

Trigonometry Worksheet - 1

Trigonometry Worksheet - 2

Trigonometry Worksheet - 3

Answer Sheet

Trigonometry-AnswerDownload the pdf

Copyright © 2024 LetsPlayMaths.com. All Rights Reserved.
Email: feedback@letsplaymaths.com